はじめに

『ガウス過程と機械学習』 を 3 度ほど読んでいるけれども、直観的な理解までは至っていないので、要所をプログラムをに落としながら読み進めてみます。
とりあえず、3 章まで試してみます。

実装は分かりやすさ重視で、なるべく書籍の内容と整合性が取れるようにします。

1.1 単回帰

データを与えられた時の単回帰について。

内容は公式 1.1 の導出が主眼なので、与えられたデータについて、公式 1.1 を用いて回帰式を計算して、プロットしてみます。

実行すると下のグラフが作図されます。

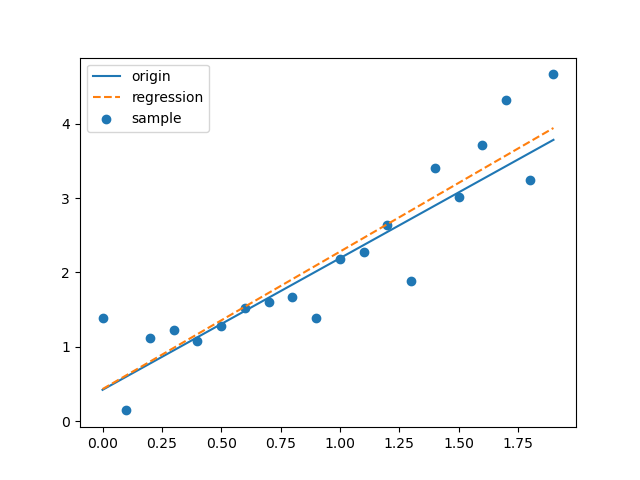
青実線が理論値、青点が理論値からサンプルしノイズを付加したデータ、オレンジ破線が導出した回帰式です。

1.2 重回帰とベクトル表現

重回帰モデルを導出するのが主眼。

書籍中の図 1.7 の 2 次元データを与えて、回帰平面を出力してみます。

実行すると下のグラフが作図されます。

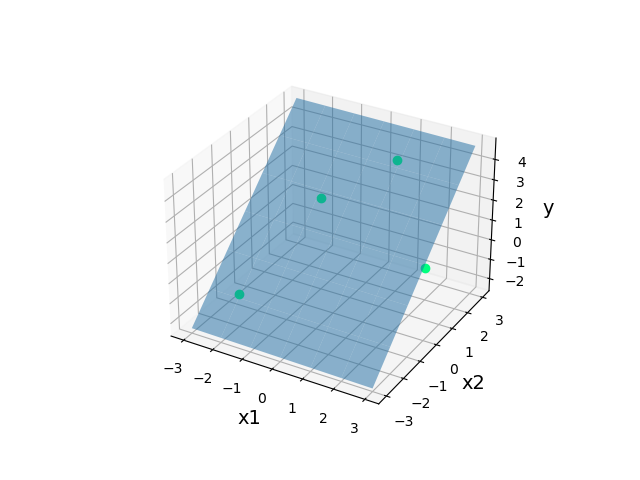
緑点がデータ、青平面が回帰平面です。

まだ気にする場面は少ないですが、本書ではデータの集合は列ベクトルとして与えられることに注意。

1.3 線形回帰モデル

重回帰を拡張して、非線形なデータに対しても回帰式を得られるようにするのが主眼。

ノイズ交じりの非線形なデータを与えて、特徴ベクトルを用いた線形回帰を導出します。

実行結果はこちら。

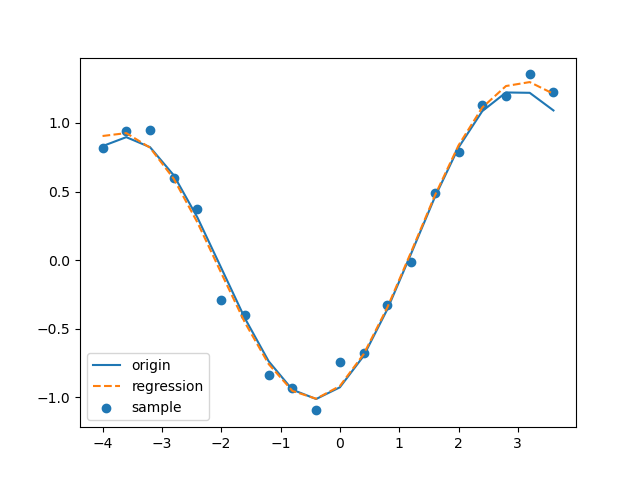
1-1.py と同様に、青実線が理論値、青点がノイズを付加したサンプル、オレンジ破線が回帰式です。

1.4 リッジ回帰

リッジ つまり峰により結果が不安定になることを防ぐ回帰。

公式 1.6 の導出と理解が主眼。
微小な対角成分を負荷して、多重共線性を避ける。

多重共線性のあるデータを入力として与えて、回帰式の重み w を取得します。

実行結果は、回帰式の重み w の数値データです。
[-0.65610355 0.17853158 0.35706316] となり、確かに多重共線性の問題が回避されていることが確認できます。

参考・リンク

GitHub : https://github.com/AmanouToona/GPandML